Constructing ZDDs
Given a family \(F\) of sets, we can find its ZDD as follows.
-
If \(F = \emptyset\) (\(F\) is empty) return \(\bot\). If \(F = \epsilon\) (\(F\) contains only the empty set) then return \(\top\).
-
Find the smallest element \(v\) amongst all elements in all sets of \(F\). Create a node \(v\).
-
Let \(F_0\) be the family of all sets in \(F\) not containing \(v\), that is, \( F_0 = \{ \alpha : \alpha \in F, v \notin \alpha \} \). Recursively construct the ZDD for \(F_0\), and connect the LO edge from \(v\) to the root of \(F_0\).
-
Let \(F_1\) be the family resulting from taking all sets in \(F\) that contain \(v\) and then removing \(v\) from each set: \( F_1 = \{ \alpha\setminus\{v\} : \alpha \in F, v \in \alpha \} \). Recursively construct the ZDD for \(F_1\), and connect the HI edge from \(v\) to the root of \(F_1\).
-
Look for identical nodes (same label, same LO desination and same HI destination) and combine them.
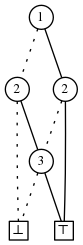
Some families have special properties allowing their ZDDs to be immediately constructed. In a universe of size \(n\), consider for example the family of all sets of size \(k\) which we denote \(S_k(\{1,...,n\})\). The ZDD of \(S_2(\{1,2,3\}) = \{ \{1,2\}, \{2,3\}, \{1,3\}\}\) is the following:

The ZDD of \(S_k(\{1,...,n\})\) turns out to be easy to describe (exercise).
Here are some more examples. Let \(U = \{1, ..., 6\}\) and \(S = \{2,3,5\}\). The ZDD of all subsets of \(U\) containing exactly one element of \(S\) is:
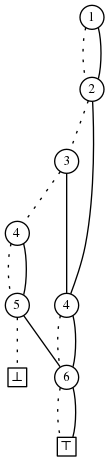
The ZDD of all sets containing at least one element of \(S\) is:

The ZDD of all sets containing at most one element of \(S\) is:
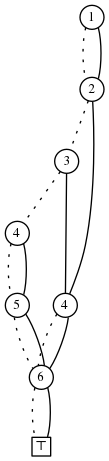
These 3 examples are readily generalized. Each can be viewed as a ZDD of all sets that branches off at the smallest element of \(S\), before joining the main branch again after the largest element of \(S\) has been handled.
In many combinatorial problems, we start with families that can be immediately written down. We then perform operations on these families to construct other families which we use to solve the problem. For example, given ZDDs \(F\) and \(G\), we construct \(F \cup G\), or \(F \cap G\), or \(F\sqcup G\), or similar.