1. Consider the following encryption scheme for n-letter messages. The secret key corresponds to a permutation on n locations. Given a message , one computes its encryption by

   

   For example, suppose that 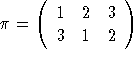. That is , and . Then the encryption would be ``nDa''.

   A.

   How does the security of this scheme vary according to the message size?

   B.

   What information is leaked by a single encryption using this scheme? That is, given 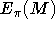, what can we determine about M.

   Now let's try to break this scheme completely given multiple encryptions 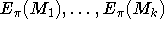for a fixed key . We assume that we don't know 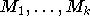a priori but that they are in english.

   C.

   For a given i and j, how might we determine whether 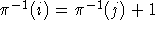, given enough messages? That is, can we determine if letters i and j of the ciphertext correspond to consecutive letters of the plaintext.

   D.

   Using the answer to Part 3, show how to reconstruct .

   E.

   Suppose that 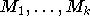were not english but instead were just random strings. Could we find given the ciphertext only?

2. Data compression is often used in data storage or transmission. Suppose you want to use data compression in conjunction with encryption. Does it make more sense to

   A.

   Compress the data and then encrypt the result, or

   B.

   Encrypt the data and then compress the result.

   Justify your answer. Try to give at least two reasons.

3. Before DESX was invented, the researchers at RSA Labs came up with DESV and DESW, defined by

   

   As with DESX, |k|=56 and . Show that both these proposals do not increase the work needed to break the cryptosystem using brute-force key search. That is, show how to break these schemes using on the order of DES encryptions/decryptions. You may assume that you have a moderate number of plaintext-ciphertext pairs, .

4. Given a cryptosystem , define the randomized cryptosystem by

   

   where R is a random bit string of the same size as the message. That is, the output of is the encryption of a random one-time pad along with the original message XORed with the random pad. A new independent random pad R is chosen for every encryption.

   We consider two attack models. The goal of both models is to reconstruct the actual secret key k.

   • In the key-reconstruction chosen plaintext attack (KR-CPA), the adversary is allowed to generate strings 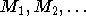and for each 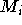learn a corresponding ciphertext.
   • In the key-reconstruction random plaintext attack (KR-RPA), the adversary receives random plaintext/ciphertext pairs.

   Note that for the case of the opponent has no control over the random pad R used in the creation of the given plaintext/ciphertext pairs.

   Prove that if is secure against KR-RPA attacks then is secure against attacks.

   [Hint: It is easiest to show the contrapositive. Given an algorithm A that executes a successful attack against , exhibit an algorithm B (using A as a ``subroutine'') that executes a successful attack against .]